Powers of 2 Cubes
I love these.

I made them (but I did not invent them). I had them 3D printed in downtown Dayton at a cool maker space. I did not save money by printing them myself.
Each cube is twice as big as the last.
You can model any number with these cubes.
42?
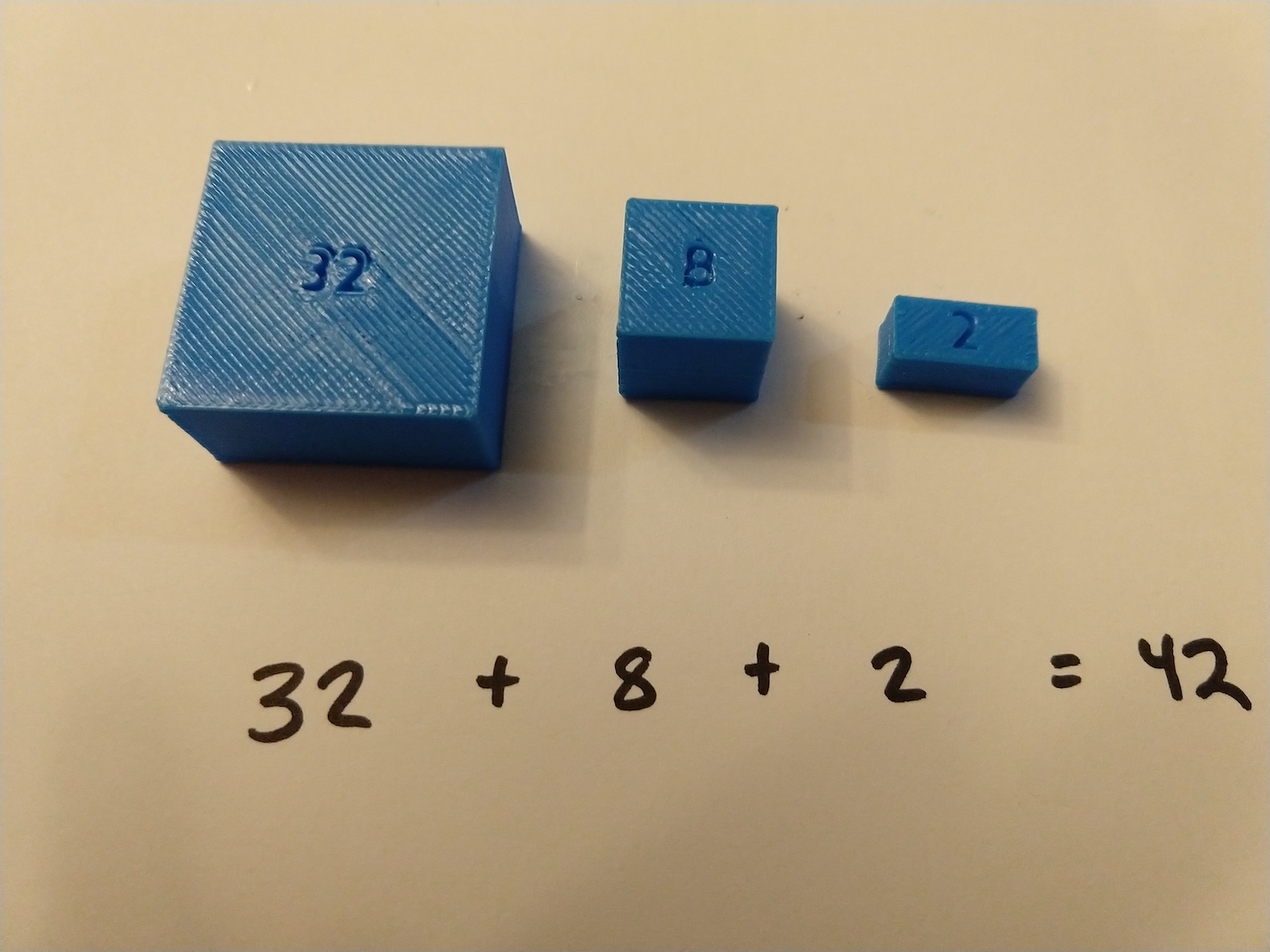
158?

It’s getting tiresome to post pictures, so I’m just going to write down how many of each cube you need. I’ll list how many you need, biggest to smallest. How many 256 cubes you need, how many 128 cubes you need, how many 64 cubes you need, how many 32s, how many 16s, how many 8s, how many 4s, how many 2s, how many 1s.
42? 000101010
158? 010011110
2047? 111111111
This is binary! Binary is a counting system with just two numbers, 0 and 1. After you say 0, then 1, you have to go up a place value and the third number you say is 10. Then 11, then 100.
It’s also called Base 2, since it has two digits. Unlike our Base Ten system has ten numbers, presumably because we have ten fingers. But it’s awful to count on your fingers, because you can only get to ten. Here’s how Peter gets to 31 on just one hand.
You can go all the way to 1023 on your fingers counting in binary.
If I stack all the blocks I have (11111) it looks like this.
 You’ll notice it’s missing one unit to be a perfect cube (100000).
You’ll notice it’s missing one unit to be a perfect cube (100000).
The cubes (or maybe math itself) makes beautiful patterns.

Are you ready to have your mind blown? All the numbers which are perfect cubes (1,8,64) are perfect cubes.

Sometimes my kids just build with the blocks, and that’s okay. They are internalizing the concepts, without knowing it. Kids learn through their fingers much better than through their ears.
I made this video of how much I love them, and it’s probably worse than the one I learned from, but I made it and now no other human being (besides my children who have no choice) has to sit and listen to me talk about my powers of 2 cubes ever again.


